Underrated Ideas Of Tips About What Is Parallel To Y 2x 2
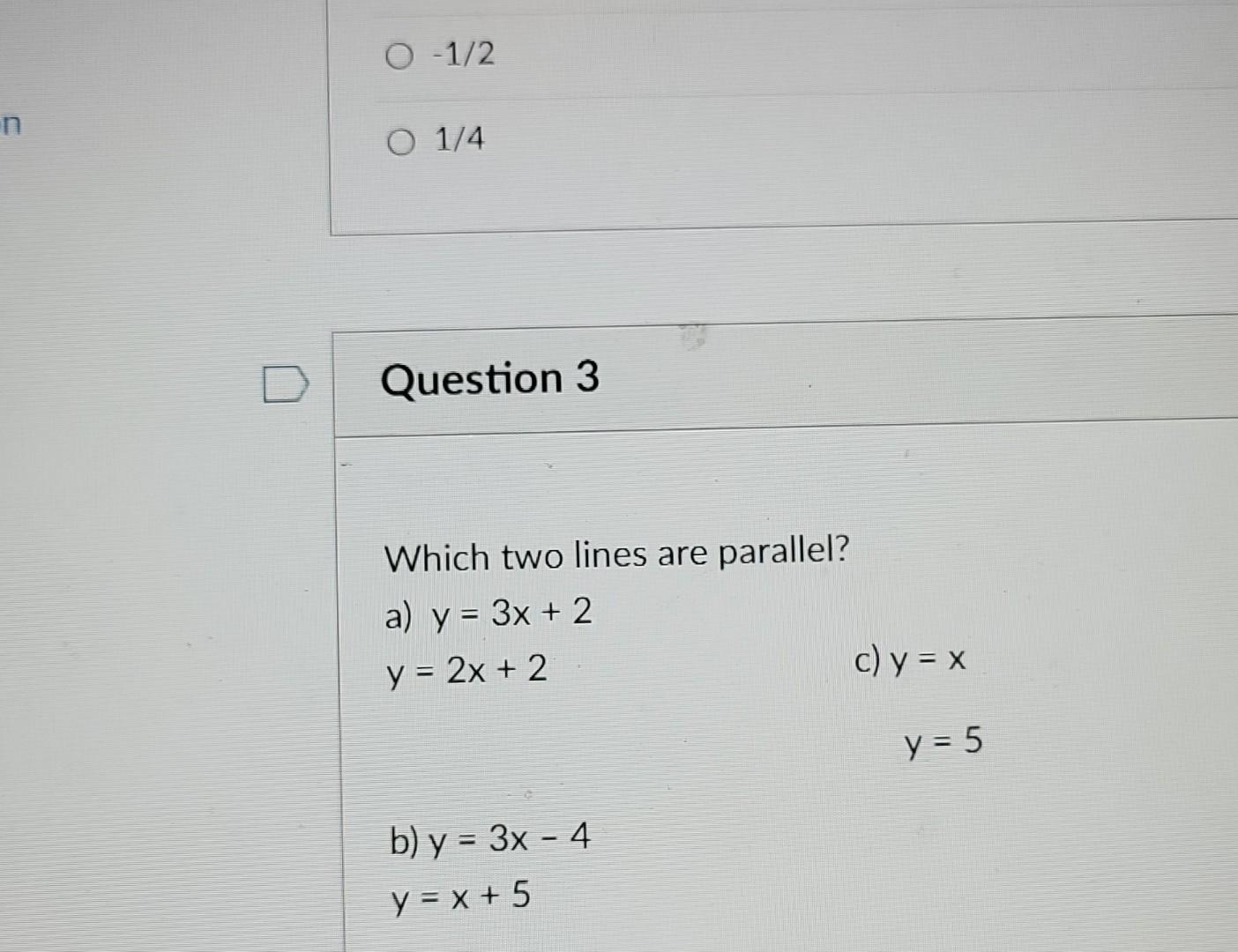
Solved Which Two Lines Are Parallel? A) Y=3x+2y=2x+2 C)
Understanding Parallel Lines in the Realm of 'y = 2x + 2'
1. Decoding the Secrets of Parallelism
Alright, let's untangle this math mystery. When we talk about lines being "parallel to y = 2x + 2," we're diving into the world of linear equations. The core concept here is that parallel lines never, ever meet. Think of railroad tracks; they run side-by-side indefinitely without crossing paths. In the language of math, what makes them stay that way is their slope.
The equation 'y = 2x + 2' is in what's called slope-intercept form. It's a super handy way to write linear equations because it tells you two very important things straight away: the slope (which is 2 in this case) and the y-intercept (which is also 2). The slope tells us how steep the line is, and the y-intercept tells us where the line crosses the y-axis.
So, any line that's parallel to 'y = 2x + 2' must have the same slope. It's like they're both climbing the same hill at the same angle. The only difference can be where they start on the y-axis. They could start higher up or lower down, but they'll still be running alongside each other, never intersecting.
Therefore, the answer to the question "What is parallel to y = 2x + 2?" is any line that has a slope of 2. It's that simple! The y-intercept can be anything you want — it just determines where the line sits on the graph. Think of it like shifting the railroad tracks up or down; they're still parallel, just in a different location.
[Solved] A Line Is Parallel To Y=2x5 And Intersects The Point (1,3
Examples of Lines Parallel to 'y = 2x + 2'
2. Putting Theory into Practice
Now that we know the secret ingredient (the slope), let's whip up a few examples of lines parallel to 'y = 2x + 2'. Remember, as long as the slope is 2, we're golden. The y-intercept is our playground for creativity.
How about 'y = 2x + 5'? This line has the same slope as 'y = 2x + 2' (which is 2), but it crosses the y-axis at 5 instead of 2. They're parallel, like two peas in a pod, just sitting at different heights.
Or consider 'y = 2x - 3'. Here, the slope is still 2, but the y-intercept is -3. This line is parallel to 'y = 2x + 2', but it's located lower down on the graph. It's like the first line decided to take the stairs down three floors, but still walks in the same direction.
One more for good measure: 'y = 2x'. This line has a y-intercept of 0 (it passes through the origin). It's still parallel to 'y = 2x + 2', but it's the basic, un-shifted version. It's like the original railroad track before anyone decided to move it up or down.

Consider The Line Y 2x 4.Find Equation Of That Is
The Importance of Slope
3. Why It's the King (or Queen) of Parallelism
You might be wondering, "Okay, okay, I get it, the slope needs to be the same. But why is that so important?" That's a great question! The slope is the key to understanding the direction and steepness of a line. It's what dictates how quickly the line rises (or falls) as you move along the x-axis.
If two lines have different slopes, it means they're heading in different directions. Eventually, no matter how close they start, they're going to intersect. It's inevitable. It's like two cars starting on the same road but turning off at different angles; they're not going to stay side-by-side for long.
But when two lines have the same slope, it means they're moving in the same direction at the same rate. They're perfectly synchronized. They're never going to get closer, and they're never going to get further apart. They're destined to remain parallel forever. They're the geometric equivalent of soulmates, except without the drama.
Think of it like a race. If two runners are running at the same speed and in the same direction, they'll stay next to each other the entire time. They're parallel! But if one runner is faster or running at a slightly different angle, they'll eventually pull ahead or cross paths. That's the power of the slope!

How To Find A Parallel Line Through Point
How to Find a Line Parallel to a Given Line
4. A Step-by-Step Guide
So, you've got a line, and you need to find another line that's parallel to it. No sweat! Here's a simple, step-by-step guide to help you find one:
Step 1: Identify the Slope. Look at the equation of the line you're given. If it's in slope-intercept form (y = mx + b), the slope is the 'm' value. If it's not in slope-intercept form, you'll need to rearrange it to get it into that form. For example, if you see 2y = 4x + 6, divide the entire equation by 2 to get y = 2x + 3. The slope is 2.
Step 2: Use the Same Slope. Now that you know the slope, use that same value for your new line. So, if the original slope was 2, your new line will start with 'y = 2x'.
Step 3: Choose a Different Y-intercept. Pick any number you want for the y-intercept (the 'b' value in y = mx + b). It can be positive, negative, zero, a fraction — whatever tickles your fancy. Just make sure it's different from the y-intercept of the original line. For example, you could choose 7, making your parallel line 'y = 2x + 7'.
Step 4: Voila! You've got a line parallel to the original line. It's like magic, but with math. Just be sure to double check your work if you are unsure and you should be right as rain!

Equation Of A Line Parallel Calculator
Real-World Applications of Parallel Lines
5. Beyond the Textbook
Parallel lines aren't just abstract concepts confined to math textbooks. They show up all over the place in the real world. Understanding them can actually be quite useful, whether you realize it or not!
Think about architecture. Buildings are full of parallel lines — walls, floors, ceilings, the edges of windows and doors. These parallel lines create a sense of order and stability. They're not just aesthetically pleasing; they're structurally important.
In urban planning, streets are often designed to be parallel, or at least close to it. This makes navigation easier and more efficient. Think of a city grid; it's a network of parallel and perpendicular lines that helps us find our way around. It also makes the city's layout much easier to build, since the basic design is easily repeatible and can easily be expanded into new areas.
Even in art and design, parallel lines play a role. They can be used to create a sense of depth and perspective. Artists use parallel lines to draw roads or buildings that seem to recede into the distance. Graphic designers use them to create patterns and textures that are both visually appealing and functional.
Graph Y 2x 0
FAQs About Parallel Lines and 'y = 2x + 2'
6. Your Burning Questions Answered
Still have some lingering questions about parallel lines? Let's tackle some frequently asked questions:
Q: What if the equation isn't in slope-intercept form?A: No problem! Just rearrange the equation to get it into the form y = mx + b. The coefficient of 'x' will be your slope.
Q: Can a line be parallel to itself?A: Technically, yes, a line is considered parallel to itself. It's like saying a mirror image is parallel to the original. But when we're talking about finding different lines that are parallel, we're looking for lines with the same slope but different y-intercepts.
Q: What about perpendicular lines? How are they different?A: Perpendicular lines intersect at a 90-degree angle. Their slopes are negative reciprocals of each other. For example, a line perpendicular to 'y = 2x + 2' would have a slope of -1/2.